Quicksort in Groovy - can it be as fast as implemented in Java?
I started reading "Cracking the Coding Interview, 6th Edition" book recently and it inspired me to experiment a bit. It’s been a while since I implemented the quicksort algorithm the last time, and I did that in Haskell. I remember some old and imperative implementations in Java, but I never tried to implement it in Groovy. Let’s give it a try!
Quicksort in Groovy
The simplest implementation of the Quicksort algorithm in Groovy may look like this.
import groovy.transform.CompileStatic
@CompileStatic
<T extends Comparable> List<T> quicksort(final List<T> list) {
if (list.size() <= 1) { (1)
return list
}
final pivot = list.head() (2)
final split = list.tail().split { el -> el < pivot } (3)
return quicksort(split.get(0)) + [pivot] + quicksort(split.get(1)) (4)
}The implementation is clean and simple. For any list of size equal or lower than 1, it returns the input list. Otherwise, it takes the first element using list.head() method, and splits the remaining list into two list — the first that contains elements that are lower than the pivot value, and the second that contains elements that are equal to or greater than the pivot value. Then it recursively calls quicksort on both lists .
We can run groovysh now to test this function with a few exemplary data sets.
$ groovysh quicksortExamples.groovy
Groovy Shell (2.5.8, JVM: 1.8.0_201)
Type ':help' or ':h' for help.
---------------------------------------------------------------------------------------------------
groovy:000> quicksort([])
===> []
groovy:000> quicksort([1])
===> [1]
groovy:000> quicksort([0,1])
===> [0, 1]
groovy:000> quicksort([1,0])
===> [0, 1]
groovy:000> random = new Random()
===> java.util.Random@64337702
groovy:000> list = (1..20).collect { random.nextInt(100) }
===> [9, 19, 41, 13, 66, 28, 12, 79, 71, 43, 6, 50, 56, 24, 84, 88, 38, 82, 36, 80]
groovy:000> quicksort(list)
===> [6, 9, 12, 13, 19, 24, 28, 36, 38, 41, 43, 50, 56, 66, 71, 79, 80, 82, 84, 88]
groovy:000>The benchmark
The implementation of the quicksort function in Groovy looks good. It’s short, clean, and simple. The only question is — is it efficient?
We can measure it with a simple "benchmark". I haven’t use JMH on purpose here, I wanted to keep everything in a single Groovy script file. I decided to implement a simple benchmark-like test that measures computation time (in milliseconds.)
import groovy.transform.CompileStatic
import groovy.transform.Field
import java.util.stream.Collectors
import java.util.stream.IntStream
@CompileStatic
<T extends Comparable> List<T> quicksort(final List<T> list) {
if (list.size() <= 1) {
return list
}
final pivot = list.head()
final split = list.tail().split { el -> el < pivot }
return quicksort(split.get(0)) + [pivot] + quicksort(split.get(1))
}
@Field
static final Random random = new Random()
@CompileStatic
private static List<List<Integer>> randomData(int numberOfLists, int listSize) {
return IntStream.range(0, numberOfLists)
.boxed()
.parallel()
.map { (1..listSize).collect { random.nextInt(1000) } }
.collect(Collectors.toList())
}
@CompileStatic
long iteration(int iterations, int size) {
final List<List<Integer>> lists = randomData(iterations, size)
final List<List<Integer>> sorted = new ArrayList<>(lists.size())
long start = System.currentTimeMillis()
for (List<Integer> it : lists) {
sorted.add(quicksort(it))
}
long time = System.currentTimeMillis() - start
println("Sorted in ${time} ms")
assert sorted.every { list -> ((List) list).toSorted() == list && ((List) list).size() == size }
return time
}
@CompileStatic
void benchmark() {
final int iterations = 1000
final int randomListSize = 1000
final int repeat = 100
final int warmup = 40
final List<Long> times = (1..repeat).collect { iteration(iterations, randomListSize) }.drop(warmup)
println ("-" * 40)
println "Average: ${(times.sum() as double) / times.size()} ms"
println "Min: ${times.min()} ms"
println "Max: ${times.max()} ms"
println "Median: ${times.sort().get((times.size() / 2).toInteger())} ms"
}
benchmark()This benchmark repeats a total of 1000 iterations 100 times. The first 40 repetitions are dropped — we treat them as a JVM warmup. Every repeated iteration produces a list of one thousand lists of one thousand random integers. Then it iterates and sorts each list of random numbers. The total time needed to sort all one thousand lists is recorder and printed out to console. The benchmark code also verifies if the quicksort implementation works — at the end of every iteration it checks if every list returned by the quicksort method is sorted.
Running quicksort.groovy script produces the output similar to this one.
$ groovy quicksort.groovy
Sorted in 1315 ms
Sorted in 1046 ms
Sorted in 930 ms
Sorted in 1077 ms
Sorted in 943 ms
Sorted in 952 ms
Sorted in 949 ms
Sorted in 919 ms
Sorted in 943 ms
Sorted in 927 ms
Sorted in 936 ms
Sorted in 932 ms
Sorted in 972 ms
Sorted in 979 ms
Sorted in 976 ms
Sorted in 982 ms
Sorted in 978 ms
Sorted in 944 ms
Sorted in 922 ms
Sorted in 921 ms
Sorted in 926 ms
Sorted in 922 ms
Sorted in 927 ms
Sorted in 924 ms
Sorted in 987 ms
Sorted in 930 ms
Sorted in 919 ms
Sorted in 926 ms
Sorted in 930 ms
Sorted in 923 ms
Sorted in 923 ms
Sorted in 928 ms
Sorted in 917 ms
Sorted in 976 ms
Sorted in 986 ms
Sorted in 985 ms
Sorted in 978 ms
Sorted in 993 ms
Sorted in 975 ms
Sorted in 936 ms
Sorted in 929 ms
Sorted in 932 ms
Sorted in 923 ms
Sorted in 920 ms
Sorted in 921 ms
Sorted in 917 ms
Sorted in 929 ms
Sorted in 927 ms
Sorted in 927 ms
Sorted in 919 ms
Sorted in 962 ms
Sorted in 939 ms
Sorted in 933 ms
Sorted in 931 ms
Sorted in 925 ms
Sorted in 933 ms
Sorted in 961 ms
Sorted in 930 ms
Sorted in 924 ms
Sorted in 924 ms
Sorted in 921 ms
Sorted in 928 ms
Sorted in 935 ms
Sorted in 918 ms
Sorted in 922 ms
Sorted in 942 ms
Sorted in 918 ms
Sorted in 927 ms
Sorted in 1018 ms
Sorted in 982 ms
Sorted in 930 ms
Sorted in 923 ms
Sorted in 923 ms
Sorted in 922 ms
Sorted in 926 ms
Sorted in 994 ms
Sorted in 1020 ms
Sorted in 1004 ms
Sorted in 1000 ms
Sorted in 1007 ms
Sorted in 1007 ms
Sorted in 1004 ms
Sorted in 1009 ms
Sorted in 995 ms
Sorted in 1005 ms
Sorted in 1007 ms
Sorted in 1003 ms
Sorted in 991 ms
Sorted in 988 ms
Sorted in 995 ms
Sorted in 987 ms
Sorted in 919 ms
Sorted in 925 ms
Sorted in 920 ms
Sorted in 918 ms
Sorted in 933 ms
Sorted in 927 ms
Sorted in 932 ms
Sorted in 921 ms
Sorted in 926 ms
----------------------------------------
Average: 949.6333333333333 ms
Min: 917 ms
Max: 1020 ms
Median: 930 msIt looks like sorting one thousand lists of one thousand random numbers with Groovy quicksort takes ~930 milliseconds. It feels like it is slow, but to decide if this is true or false, we need to compare it with something. Let’s implement using imperative Java code and see how efficient it is.
| ATTENTION: The goal of those benchmark tests is not to get specific and exact results, but rather to find an order of magnitude. |
Quicksort in Java
import java.util.ArrayList;
import java.util.List;
public final class Java {
public static <T extends Comparable> List<T> quicksort(final List<T> list) {
if (list.size() <= 1) {
return list;
}
final List<T> left = new ArrayList<>(list.size() - 1);
final List<T> right = new ArrayList<>(list.size() - 1);
final T pivot = list.get(0);
for (T el : list.subList(1, list.size())) {
if (pivot.compareTo(el) >= 0) {
left.add(el);
} else {
right.add(el);
}
}
final List<T> result = new ArrayList<>(list.size());
result.addAll(quicksort(left));
result.add(pivot);
result.addAll(quicksort(right));
return result;
}
}Here is the same algorithm implemented using imperative Java. We can replace quicksort(it) method invocation inside the iteration method to Java.quicksort(it).
$ groovyc -j Java.java quicksort.groovy
Note: /home/wololock/workspace/groovy-sandbox/src/Java.java uses unchecked or unsafe operations.
Note: Recompile with -Xlint:unchecked for details.
$ groovy quicksort
Sorted in 342 ms
Sorted in 249 ms
Sorted in 218 ms
Sorted in 241 ms
Sorted in 214 ms
Sorted in 210 ms
Sorted in 289 ms
Sorted in 202 ms
Sorted in 212 ms
Sorted in 202 ms
Sorted in 196 ms
Sorted in 294 ms
Sorted in 201 ms
Sorted in 198 ms
Sorted in 198 ms
Sorted in 215 ms
Sorted in 204 ms
Sorted in 197 ms
Sorted in 212 ms
Sorted in 208 ms
Sorted in 197 ms
Sorted in 219 ms
Sorted in 207 ms
Sorted in 200 ms
Sorted in 204 ms
Sorted in 201 ms
Sorted in 201 ms
Sorted in 204 ms
Sorted in 213 ms
Sorted in 198 ms
Sorted in 204 ms
Sorted in 213 ms
Sorted in 198 ms
Sorted in 208 ms
Sorted in 213 ms
Sorted in 198 ms
Sorted in 202 ms
Sorted in 204 ms
Sorted in 196 ms
Sorted in 205 ms
Sorted in 196 ms
Sorted in 205 ms
Sorted in 208 ms
Sorted in 195 ms
Sorted in 208 ms
Sorted in 208 ms
Sorted in 197 ms
Sorted in 211 ms
Sorted in 213 ms
Sorted in 198 ms
Sorted in 200 ms
Sorted in 211 ms
Sorted in 196 ms
Sorted in 200 ms
Sorted in 217 ms
Sorted in 199 ms
Sorted in 201 ms
Sorted in 220 ms
Sorted in 200 ms
Sorted in 200 ms
Sorted in 217 ms
Sorted in 197 ms
Sorted in 200 ms
Sorted in 204 ms
Sorted in 206 ms
Sorted in 197 ms
Sorted in 204 ms
Sorted in 210 ms
Sorted in 198 ms
Sorted in 204 ms
Sorted in 211 ms
Sorted in 200 ms
Sorted in 203 ms
Sorted in 197 ms
Sorted in 203 ms
Sorted in 205 ms
Sorted in 199 ms
Sorted in 201 ms
Sorted in 203 ms
Sorted in 198 ms
Sorted in 204 ms
Sorted in 208 ms
Sorted in 216 ms
Sorted in 205 ms
Sorted in 202 ms
Sorted in 214 ms
Sorted in 204 ms
Sorted in 201 ms
Sorted in 211 ms
Sorted in 195 ms
Sorted in 208 ms
Sorted in 215 ms
Sorted in 198 ms
Sorted in 202 ms
Sorted in 197 ms
Sorted in 194 ms
Sorted in 200 ms
Sorted in 198 ms
Sorted in 193 ms
Sorted in 203 ms
----------------------------------------
Average: 203.46666666666667 ms
Min: 193 ms
Max: 220 ms
Median: 203 msWe can see that Java implementation is approximately 4 times faster than the Groovy one.
Can Groovy do better than ~930 ms?
I started wondering what makes Groovy slower compared to Java, and if it possible to make Groovy code faster? What would Groovy do with an imperative code similar to the Java one? Let’s give it a shot. I added the quicksortImperative method to quicksort.groovy and put it inside the iteration method to measure its efficiency.
@CompileStatic
<T extends Comparable> List<T> quicksortImperative(final List<T> list) {
if (list.size() <= 1) {
return list;
}
final List<T> left = (List<T>) new ArrayList<T>(list.size() - 1);
final List<T> right = (List<T>) new ArrayList<T>(list.size() - 1);
final T pivot = list.get(0);
for (T el : list.subList(1, list.size())) {
if (pivot.compareTo(el) >= 0) {
left.add(el);
} else {
right.add(el);
}
}
final List<T> result = new ArrayList<>(list.size());
result.addAll(quicksortImperative(left));
result.add(pivot);
result.addAll(quicksortImperative(right));
return result;
}And here is the benchmark result.
$ groovy quicksort
Sorted in 341 ms
Sorted in 260 ms
Sorted in 224 ms
Sorted in 242 ms
Sorted in 222 ms
Sorted in 210 ms
Sorted in 292 ms
Sorted in 208 ms
Sorted in 224 ms
Sorted in 212 ms
Sorted in 212 ms
Sorted in 308 ms
Sorted in 210 ms
Sorted in 214 ms
Sorted in 209 ms
Sorted in 223 ms
Sorted in 213 ms
Sorted in 208 ms
Sorted in 228 ms
Sorted in 211 ms
Sorted in 208 ms
Sorted in 231 ms
Sorted in 209 ms
Sorted in 208 ms
Sorted in 213 ms
Sorted in 205 ms
Sorted in 209 ms
Sorted in 220 ms
Sorted in 219 ms
Sorted in 212 ms
Sorted in 217 ms
Sorted in 222 ms
Sorted in 215 ms
Sorted in 209 ms
Sorted in 223 ms
Sorted in 209 ms
Sorted in 208 ms
Sorted in 206 ms
Sorted in 201 ms
Sorted in 214 ms
Sorted in 211 ms
Sorted in 223 ms
Sorted in 209 ms
Sorted in 207 ms
Sorted in 224 ms
Sorted in 212 ms
Sorted in 206 ms
Sorted in 212 ms
Sorted in 214 ms
Sorted in 212 ms
Sorted in 208 ms
Sorted in 215 ms
Sorted in 211 ms
Sorted in 206 ms
Sorted in 221 ms
Sorted in 211 ms
Sorted in 205 ms
Sorted in 222 ms
Sorted in 213 ms
Sorted in 207 ms
Sorted in 214 ms
Sorted in 215 ms
Sorted in 213 ms
Sorted in 222 ms
Sorted in 211 ms
Sorted in 213 ms
Sorted in 220 ms
Sorted in 213 ms
Sorted in 217 ms
Sorted in 238 ms
Sorted in 206 ms
Sorted in 205 ms
Sorted in 227 ms
Sorted in 206 ms
Sorted in 208 ms
Sorted in 220 ms
Sorted in 205 ms
Sorted in 210 ms
Sorted in 217 ms
Sorted in 204 ms
Sorted in 209 ms
Sorted in 222 ms
Sorted in 216 ms
Sorted in 221 ms
Sorted in 233 ms
Sorted in 219 ms
Sorted in 225 ms
Sorted in 207 ms
Sorted in 207 ms
Sorted in 205 ms
Sorted in 211 ms
Sorted in 206 ms
Sorted in 205 ms
Sorted in 205 ms
Sorted in 208 ms
Sorted in 202 ms
Sorted in 225 ms
Sorted in 210 ms
Sorted in 203 ms
Sorted in 226 ms
----------------------------------------
Average: 213.3 ms
Min: 202 ms
Max: 238 ms
Median: 212 msHmm, Groovy imperative code is as fast as the Java one. What makes the Groovy 4-line implementation so much slower compared to this one?
Here is the root cause:
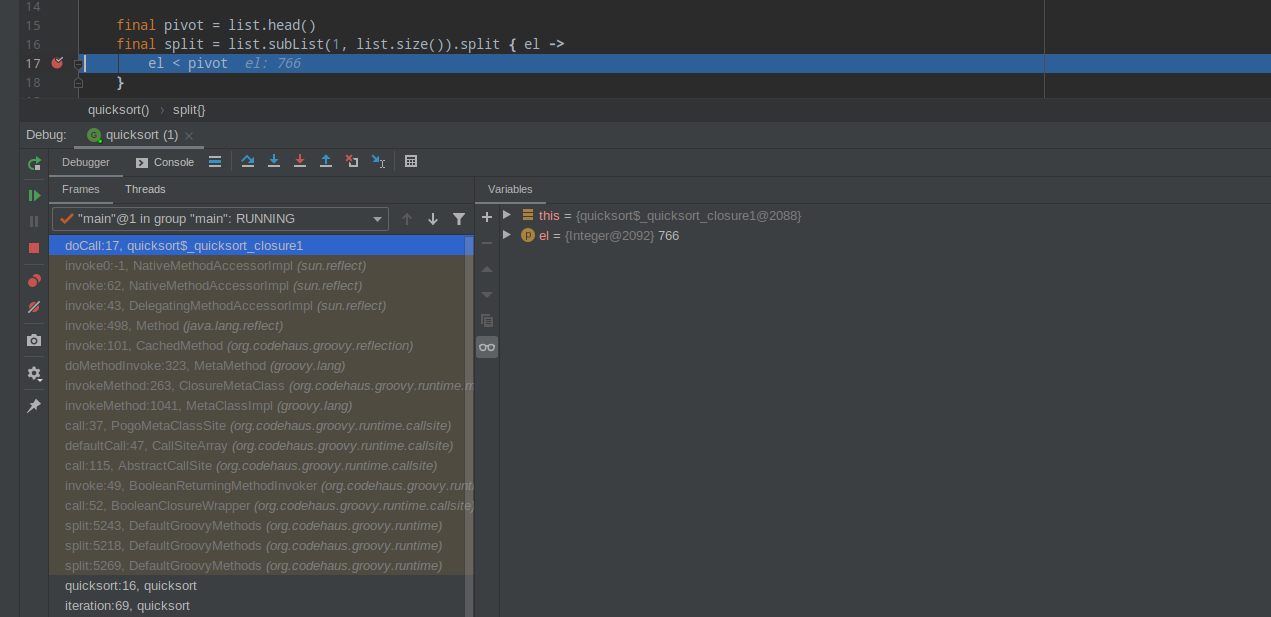
final split = list.tail().split { el -> el < pivot }If we replace it with the for-each loop presented in the Java imperative example, it runs as fast as Java’s quicksort. If you read my blog post that explains the most efficient iterations in Groovy, you already know that a for-each loop is one of the most effective ways to iterate collections in both, Groovy and Java. Invoking the list.split(closure) method comes with a price. Here you can see what the call stack looks like when we attach a breakpoint inside the closure body.
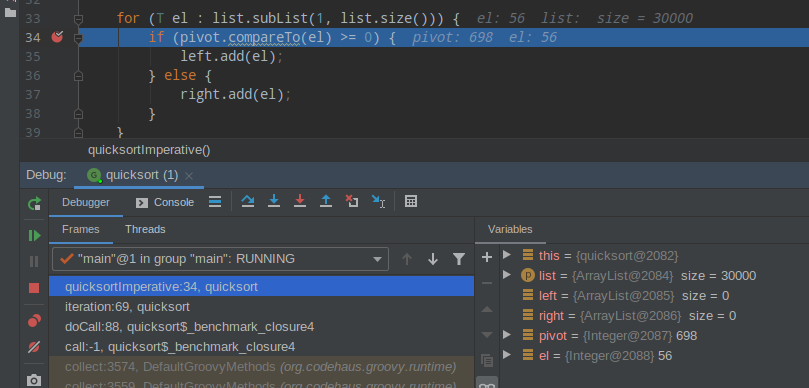
And here is the imperative equivalent.
Is the slower Groovy Quicksort a problem?
It depends. For relatively small collections, the difference between Groovy and Java implementations may be barely noticeable. For instance, if we run a single quicksort on a random list of one thousand integers, Java would sort it in ~0.5 ms while Groovy will need ~1 ms. If your program would have to process large volumes of data, and you will search for any smallest optimizations, then you would probably go with the Java option. But if you use Groovy in Spock tests, Jenkins pipelines, or even with your Grails application, that handles a relatively small amount of data to process, you don’t have to rewrite your short and simple Groovy code to get those extra 1-5 milliseconds. The clean code that developers read daily is much more important than that.
What do you think about it? Do you see an area for improvements? Would you implement a quicksort algorithm differently? Please share your thoughts in the comments section down below.

0 Comments