Tail-recursive methods in Groovy

Most of the object-oriented programmers prefer constructing algorithms using imperative style over using recursion. This is pretty obvious in the JVM ecosystem, where imperative iteration is much more efficient than recursive function call chain. However, what if I tell you that in Groovy you can take advantage of clean tail-recursive functions without sacrificing performance? Interested? Let’s deep dive into it.

Author
Szymon Stepniak
Published
Nov 12, 2018
Reading time
6 minutes
Discussion
0 Comments

Factorial function

Calculating factorial of a given number is one of the most popular recursive algorithms examples. In general, this function looks like this:

Listing 1. Exemplary factorial function implementation in Groovy

package factorial

import groovy.transform.CompileStatic
import groovy.transform.TypeChecked

@CompileStatic
@TypeChecked
class Groovy {

    static BigInteger factorial(int number) {
        if (number == 1) {
            return 1
        }
        return number * factorial(number - 1)
    }
}

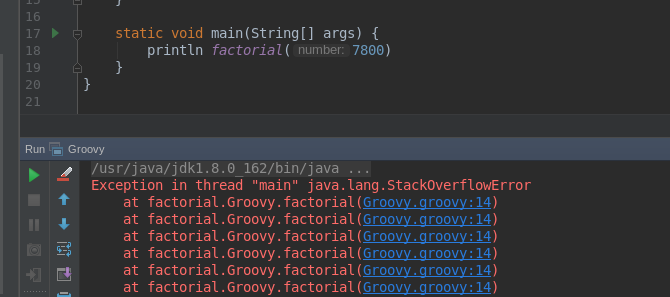
The beauty of this example is that it is concise and straightforward. However, it comes with a cost - every recursive call adds a new frame to the call stack, and we can hit stack size limit quickly. JVM crashes with StackOverflowError when it happens. For instance, calculating factorial of number 7,800 hits the stack size limit (the default 1024k for OpenJDK 1.8.0_162).

The limitation of a recursive method call depends on stack size (JVM’s -Xss option) and its current usage load (e.g., an application that executes multiple recursive functions in parallel may crash for much smaller numbers for the same stack size). The default stack size for OpenJDK 1.8.0_162 is 1024k.

Applying tail recursion

The first thing we can do to optimize our factorial function implementation is to apply tail recursion^[1]. Using tail call has one significant advantage - it does not require adding a new frame to the call stack, because all computation is done at the moment of executing recursive call. The tail-recursive function requires calling itself at the end and nothing else. Here is what tail-recursive factorial function may look like:

Listing 2. Tail-recursive factorial implemented in Groovy

package factorial

import groovy.transform.CompileStatic
import groovy.transform.TypeChecked

@CompileStatic
@TypeChecked
class Groovy {

    static BigInteger factorial(int number, BigInteger acc = 1) {
        if (number == 1) {
            return acc
        }
        return factorial(number - 1, acc.multiply(BigInteger.valueOf(number)))
    }
}

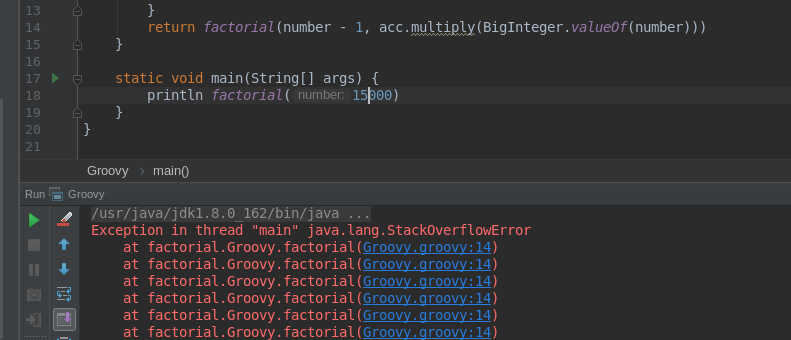
The main difference is that the tail call passes the current result of calculation recursively (usually it’s called accumulator) and it returns the calculated value when the stop condition is satisfied. Let’s run a few experiments with tail-recursive variant and see if hits the same StackOverflowError as the previous example:

As you can see, we are still affected by hitting stack size limit problems for larger numbers. It happens because the compiler does not optimize tail-recursive calls, and probably never will^[2].

Groovy’s `@TailRecursive`

Groovy introduced a new useful annotation in version 2.3 - @TailRecursive ^[3]. Without further ado, let’s add this annotation to our example and see how it works.

Listing 3. An example of @TailRecursive annotation usage in Groovy

package factorial

import groovy.transform.CompileStatic
import groovy.transform.TailRecursive
import groovy.transform.TypeChecked

@CompileStatic
@TypeChecked
class Groovy {

    @TailRecursive
    static BigInteger factorial(int number, BigInteger acc = 1) {
        if (number == 1) {
            return acc
        }
        return factorial(number - 1, acc.multiply(BigInteger.valueOf(number)))
    }
}

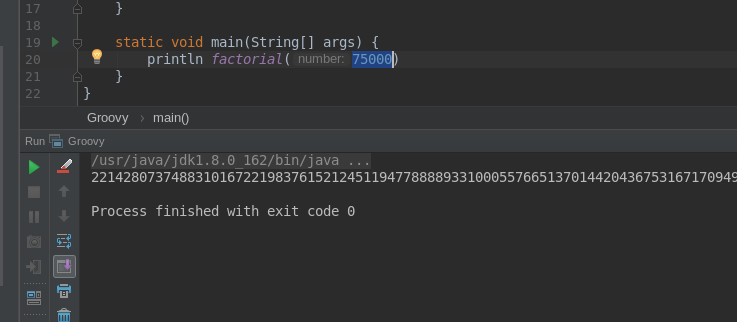
Let’s see if we can calculate factorial of number 75,000:

It didn’t crash, and it calculated a number of 333,062 digits length. How is it even possible, when the same function without annotation crashes for number 15,000? The answer is relatively simple - Groovy unraveled the code of our tail-recursive function and replaced it with an iterative equivalent. If we decompile the bytecode to a Java code we will find something similar to this one:

Listing 4. Decompiled @TailRecursive method

//
// Source code recreated from a .class file by IntelliJ IDEA
// (powered by Fernflower decompiler)
//

package factorial;

import groovy.lang.GroovyObject;
import groovy.lang.MetaClass;
import java.math.BigInteger;
import org.codehaus.groovy.runtime.ScriptBytecodeAdapter;
import org.codehaus.groovy.runtime.dgmimpl.NumberNumberMultiply;
import org.codehaus.groovy.transform.tailrec.GotoRecurHereException;

public class Groovy implements GroovyObject {
    public Groovy() {
        MetaClass var1 = this.$getStaticMetaClass();
        this.metaClass = var1;
    }

    public static BigInteger factorial(int number, BigInteger acc) {
        BigInteger _acc_ = acc;
        int _number_ = number;

        try {
            while(true) {
                try {
                    while(_number_ != 1) {
                        int __number__ = _number_;
                        int var7 = _number_ - 1;
                        _number_ = var7;
                        Number var8 = NumberNumberMultiply.multiply(__number__, _acc_);
                        _acc_ = (BigInteger)ScriptBytecodeAdapter.castToType(var8, BigInteger.class);
                    }

                    BigInteger var4 = _acc_;
                    return var4;
                } catch (GotoRecurHereException var13) {
                    ;
                }
            }
        } finally {
            ;
        }
    }

    public static BigInteger factorial(int number) {
        return factorial(number, (BigInteger)ScriptBytecodeAdapter.castToType(1, BigInteger.class));
    }
}

@TailRecursive annotation can be applied only to a function that uses tail call.

Testing `@TailRecursive` performance

Before we close this article, let’s make a quick performance test to see if it is worth using tail-recursive functions in Groovy. We use JMH tool to run the benchmark, and we compare two variants:

Groovy tail-recursive factorial function
Java imperative iteration factorial variant

Listing 5. src/main/groovy/factorial/Groovy.groovy

package factorial

import groovy.transform.CompileStatic
import groovy.transform.TailRecursive
import groovy.transform.TypeChecked

@CompileStatic
@TypeChecked
class Groovy {

    @TailRecursive
    static BigInteger factorial(int number, BigInteger acc = 1) {
        if (number == 1) {
            return acc
        }
        return factorial(number - 1, acc.multiply(BigInteger.valueOf(number)))
    }
}

Listing 6. src/main/java/factorial/Java.java

package factorial;

import java.math.BigInteger;

public class Java {

    static BigInteger factorial(int number) {
        BigInteger result = BigInteger.ONE;
        for (int i = 1; i <= number; i++) {
            result = result.multiply(BigInteger.valueOf(i));
        }
        return result;
    }
}

Here is the benchmark test case:

Listing 7. src/jmh/groovy/factorial/FactorialBench.groovy

package factorial

import groovy.transform.CompileStatic
import groovy.transform.TypeChecked
import org.openjdk.jmh.annotations.Benchmark
import org.openjdk.jmh.annotations.Scope
import org.openjdk.jmh.annotations.State

@State(Scope.Benchmark)
@CompileStatic
@TypeChecked
class FactorialBench {

    @Benchmark
    BigInteger groovy_TailRecursive_factorial_25_000() {
        return Groovy.factorial(25000)
    }

    @Benchmark
    BigInteger groovy_TailRecursive_factorial_1_000() {
        return Groovy.factorial(1000)
    }

    @Benchmark
    BigInteger java_iterative_factorial_25_000() {
        return Java.factorial(25000)
    }

    @Benchmark
    BigInteger java_iterative_factorial_1_000() {
        return Java.factorial(1000)
    }
}

Here are the results:

Listing 8. JMH benchmark results

# JMH version: 1.21
# VM version: JDK 1.8.0_162, Java HotSpot(TM) 64-Bit Server VM, 25.162-b12
# VM invoker: /usr/java/jdk1.8.0_162/jre/bin/java
# VM options: <none>
# Warmup: 1 iterations, 30 s each
# Measurement: 120 iterations, 1 s each
# Timeout: 10 min per iteration
# Threads: 1 thread, will synchronize iterations
# Benchmark mode: Average time, time/op

Benchmark                                             Mode  Cnt    Score    Error  Units
FactorialBench.groovy_TailRecursive_factorial_1_000   avgt  120    0,209 ±  0,001  ms/op
FactorialBench.groovy_TailRecursive_factorial_25_000  avgt  120  148,170 ±  0,330  ms/op
FactorialBench.java_iterative_factorial_1_000         avgt  120    0,173 ±  0,001  ms/op
FactorialBench.java_iterative_factorial_25_000        avgt  120  129,951 ±  0,321  ms/op

Full log: wololock/bec6c6cd09c80a2868eca8cce7a016a2

Laptop specs: JDK 1.8.0_162 (Java HotSpot™ 64-Bit Server VM, 25.162-b12), Groovy 2.4.12, Intel® Core™ i7-4900MQ CPU @ 2.80GHz (4 cores, cache size 8192 KB), 16 GB RAM, OS: Fedora 26 (64 bit)

Java is still faster than Groovy tail-recursive function. The first one offers the best performance, while the second one allows using tail-recursive constructs in your code with just a small (and in most cases acceptable) performance cost. I think this is a reasonable compromise between efficiency and code readability.

Conclusion

That’s it for today. I hope you have learned something useful from this article. If there is anything you would like to learn more about Groovy and its useful features, please let me know in the comments section below. Hope to see you next time!

1. https://en.wikipedia.org/wiki/Tail_call

2. https://softwareengineering.stackexchange.com/questions/272061/why-doesnt-java-have-optimization-for-tail-recursion-at-all

3. http://docs.groovy-lang.org/2.4.15/html/gapi/groovy/transform/TailRecursive.html

Tail-recursive methods in Groovy

Factorial function

Applying tail recursion

Groovy’s `@TailRecursive`

Testing `@TailRecursive` performance

Conclusion

Continue reading: "List of combinations from a list of lists in Groovy"

Groovy Trampoline Closure - a step into recursive closures

What is the most efficient way to iterate collection in Groovy? Let's play with JMH!

Groovy Regular Expressions - The Benchmark (Part 2)

0 Comments

Tail-recursive methods in Groovy

Factorial function

Applying tail recursion

Groovy’s @TailRecursive

Testing @TailRecursive performance

Conclusion

Consider buying me a coffee

Continue reading: "List of combinations from a list of lists in Groovy"

Groovy Trampoline Closure - a step into recursive closures

What is the most efficient way to iterate collection in Groovy? Let's play with JMH!

Groovy Regular Expressions - The Benchmark (Part 2)

0 Comments

Groovy’s `@TailRecursive`

Testing `@TailRecursive` performance